Hypothesis Testing on Ti 84 When You Dont Know the Standard Deviation

One sample T-Exam tests if the given sample of observations could have been generated from a population with a specified mean.

If it is found from the exam that the ways are statistically different, we infer that the sample is unlikely to take come from the population.

For case: If you want to test a car manufacturer'due south claim that their cars requite a highway mileage of 20kmpl on an average. Yous sample 10 cars from the dealership, measure out their mileage and use the T-exam to decide if the manufacturer's merits is true.

By end of this, you will know when and how to do the T-Examination, the concept, math, how to ready the null and alternate hypothesis, how to employ the T-tables, how to empathize the one-tailed and 2-tailed T-Exam and encounter how to implement in R and Python using a practical instance.

1. Introduction
2. Purpose of One Sample T Test
3. How to set the null and alternate hypothesis?
4. Use Cases
5. Process to exercise One Sample T Exam
6. One Sample T Test Case
7. One Sample T Examination Implementation
8. How to make up one's mind which T Test to perform? Two Tailed, Upper Tailed or Lower Tailed?
9. Conclusion
10. Related Posts

Introduction

The 'One sample T Examination' is one of the three types of T Tests. It is used when you desire to test if the hateful of the population from which the sample is drawn is of a hypothesized value. You volition sympathise this argument better (and all of about Ane Sample T examination) better by the end of this post.

T Test was first invented by William Sealy Gosset, in 1908. Since he used the pseudo proper name equally 'Pupil' when publishing his method in the paper titled 'Biometrika', the test came to exist know equally Student's T Exam.

Since it assumes that the test statistic, typically the sample hateful, follows the sampling distribution, the Student's T Test is considered as a Parametric test.

Purpose of I Sample T Test

The purpose of the 1 Sample T Test is to determine if a sample observations could have come from a process that follows a specific parameter (like the mean).

Information technology is typically implemented on small samples.

For example, given a sample of 15 items, you want to examination if the sample mean is the aforementioned as a hypothesized mean (population). That is, essentially you desire to know if the sample came from the given population or not.

Allow's suppose, you lot want to test if the mean weight of a manufactured component (from a sample size 15) is of a detail value (55 grams), with a 99% confidence.

How did we determine One sample T-test is the right examination for this?

Considering, in that location is only one sample involved and y'all desire to compare the hateful of this sample against a item (hypothesized) value..

To do this, yous need to set upwards a null hypothesis and an alternating hypothesis.

How to gear up the nothing and alternate hypothesis?

The null hypothesis usually assumes that at that place is no deviation in the sample means and the hypothesized hateful (comparing mean). The purpose of the T Examination is to test if the null hypothesis tin be rejected or non.

Depending on the how the problem is stated, the alternate hypothesis can be one of the following three cases:

1. 1. Case i: H1 : x̅ != µ. Used when the true sample mean is non equal to the comparison mean. Use Two Tailed T Test.

1. 1. Example two: H1 : x̅ > µ. Used when the true sample mean is greater than the comparison mean. Use Upper Tailed T Test.

1. Case three: H1 : x̅ < µ. Used when the true sample hateful is lesser than the comparison mean. Utilise Lower Tailed T Examination.

Where x̅ is the sample mean and µ is the population mean for comparison. We volition get more into the item of these iii cases afterward solving some practical examples.

Use Cases

Example i: A customer service company wants to know if their support agents are performing on par with industry standards.

According to a report the standard mean resolution time is xx minutes per ticket. The sample grouping has a mean at 21 minutes per ticket with a standard deviation of 7 minutes.

Tin you tell if the company's support performance is better than the industry standard or not?

Instance ii: A farming visitor wants to know if a new fertilizer has improved crop yield or not.

Historic information shows the average yield of the farm is 20 tonne per acre. They decide to test a new organic fertilizer on a smaller sample of farms and observe the new yield is 20.175 tonne per acre with a standard deviation of iii.02 tonne for 12 different farms.

Did the new fertilizer work?

Procedure to do 1 Sample T Test

Footstep 1: Define the Naught Hypothesis (H0) and Alternating Hypothesis (H1)

Example:

H0: Sample mean (x̅) = Hypothesized Population hateful (µ)

H1: Sample mean (x̅) != Hypothesized Population hateful (µ)

The alternate hypothesis can also land that the sample mean is greater than or less than the comparison mean.

Footstep 2: Compute the exam statistic (T)

$$t = \frac{Z}{southward} = \frac{\bar{X} – \mu}{\frac{\hat{\sigma}}{\sqrt{n}}}$$

where s is the standard error.

Step 3: Notice the T-critical from the T-Table

Utilise the degree of liberty and the blastoff level (0.05) to find the T-disquisitional.

Pace four: Determine if the computed test statistic falls in the rejection region.

Alternately, but compute the P-value. If it is less than the significance level (0.05 or 0.01), reject the null hypothesis.

One Sample T Test Case

Trouble Statement:

We have the spud yield from 12 different farms. We know that the standard white potato yield for the given diverseness is µ=xx.

x = [21.v, 24.5, xviii.v, 17.2, xiv.5, 23.2, 22.1, 20.5, 19.4, xviii.1, 24.1, 18.v]

Exam if the white potato yield from these farms is significantly better than the standard yield.

Solution:

Footstep one: Define the Cypher and Alternate Hypothesis

H0: x̅ = twenty

H1: x̅ > xx

n = 12. Since this is one sample T test, the degree of liberty = n-ane = 12-1 = xi.

Permit's set alpha = 0.05, to see 95% confidence level.

Pace 2: Calculate the Test Statistic (T)
1. Summate sample hateful

$$\bar{X} = \frac{x_1 + x_2 + x_3 + . . + x_n}{n}$$

$$\bar{10} = xx.175$$

1. Calculate sample standard deviation

$$\bar{\sigma} = \frac{(x_1 – \bar{x})^2 + (x_2 – \bar{x})^2 + (x_3 – \bar{x})^2 + . . + (x_n – \bar{x})^2}{due north-1}$$

$$\sigma = three.0211$$

1. Substitute in the T Statistic formula

$$T = \frac{\bar{x} – \mu}{se} = \frac{\bar{10} – \mu}{\frac{\sigma}{\sqrt{due north}}}$$

$$T = (20.175 – 20)/(iii.0211/\sqrt{12}) = 0.2006$$

Stride 3: Notice the T-Disquisitional

Confidence level = 0.95, alpha=0.05. For one tailed test, wait under 0.05 cavalcade. For d.o.f = 12 – 1 = 11, T-Disquisitional = 1.796.

Now you might wonder why '1 Tailed test' was called. This is considering of the mode you define the alternate hypothesis. Had the null hypothesis just stated that the sample means is non equal to twenty, so we would have gone for a two tailed exam. More than details almost this topic in the side by side department.

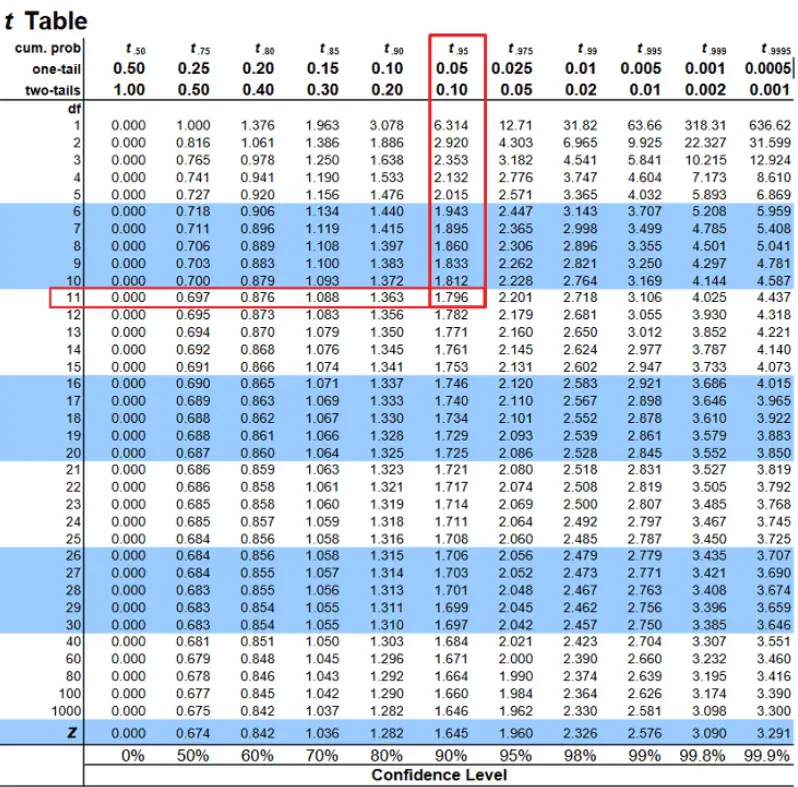
Step 4: Does it fall in rejection region?

Since the computed T Statistic is less than the T-critical, it does non autumn in the rejection region.

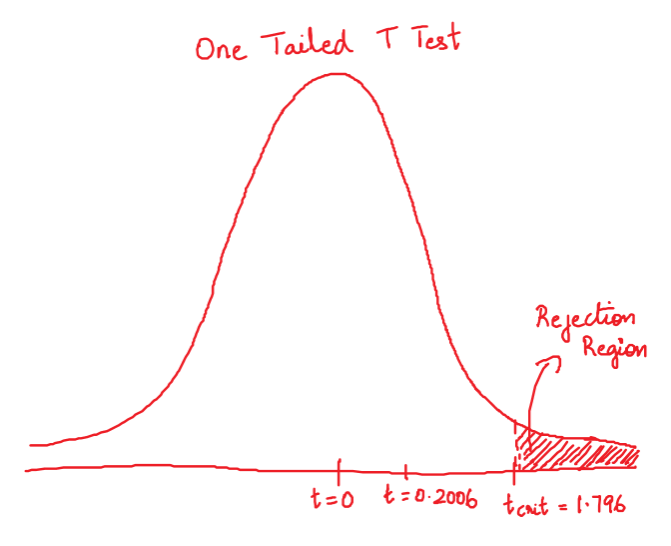
Clearly, the calculated T statistic does non fall in the rejection region. And then, we practice not reject the null hypothesis.

Ane Sample T Test Implementation

In R

Since yous want to perform a 'One Tailed Greater than' examination (that is, the sample hateful is greater than the comparison mean), you need to specify alternative='greater' in the t.test() function. Because, past default, the t.examination() does a two tailed test (which is what y'all do when your alternate hypothesis simply states sample hateful != comparison mean).

          10 <-  c(21.5,            24.5,            eighteen.5,            17.2,            xiv.5,            23.2,            22.1,            20.5,            19.4,            18.one,            24.ane,            xviii.5) t.exam(10=ten, mu=twenty, culling =            'greater')            #>     One Sample t-test            #> information:  x            #> t = 0.20066, df = 11, p-value = 0.4223            #> alternative hypothesis: true mean is greater than twenty            #> 95 percent conviction interval:            #>  18.60874      Inf            #> sample estimates:            #> mean of x                        #>    xx.175                  

The P-value computed here is nothing but p = Pr(T > t) (upper-tailed), where t is the calculated T statistic.

In Python

In Python, One sample T Test is implemented in ttest_1samp() function in the scipy bundle. However, it does a Two tailed exam by default, and reports a signed T statistic. That means, the reported P-value will always be computed for a Two-tailed test. To calculate the right P value, you need to separate the output P-value by 2.

Apply the following logic if y'all are performing a one tailed test:

For greater than test: Turn down H0 if p/ii < blastoff (0.05). In this case, t will be greater than 0.
For bottom than test: Refuse H0 if p/ii < blastoff (0.05). In this case, t will be less than 0.

          from scipy.stats            import ttest_1samp x =  [21.5,            24.5,            xviii.v,            17.2,            14.v,            23.two,            22.1,            xx.v,            19.four,            18.i,            24.1,            18.5] tscore, pvalue = ttest_1samp(x, popmean=20)                          impress              ("t Statistic: ", tscore)                                      print              ("P Value: ", pvalue)                        #> t Statistic:            0.2006562773994862            #> P Value:            0.8446291893053613                  

Since information technology is ane tailed test, the real p-value is 0.8446/2 = 0.4223. Nosotros do not rejecting the Nix Hypothesis anyway.

How to make up one's mind which T Test to perform? 2 Tailed, Upper Tailed or Lower Tailed?

The decision of whether the computed test statistic falls in the rejection region depends on how the alternating hypothesis is defined.

We know the Null Hypothesis is H0: µD = 0. Where, µD is the deviation in the ways, that is sample hateful minus the comparing hateful.

You tin can as well write H0 as: x̅ = µ, where x̅ is sample mean and 'µ' is the comparison mean.

Case 1: If H1 : x̅ != µ, then rejection region lies on both tails of the T-Distribution (two-tailed). This means the alternate hypothesis merely states the deviation in means is not equal. There is no comparison if one of the means is greater or lesser than the other.

In this case, use 2 Tailed T Examination.

Here, P value = 2 . Pr(T > | t |)

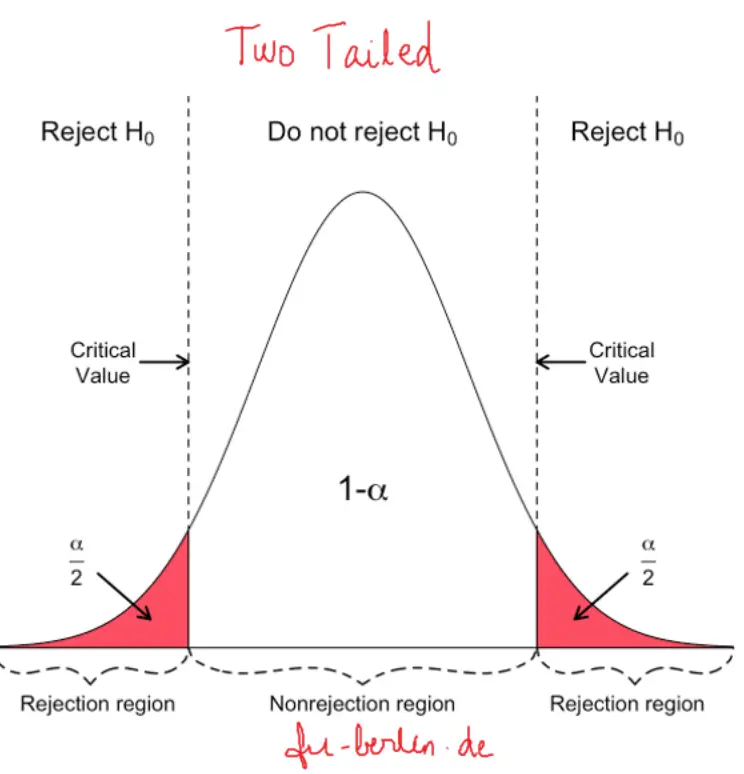
Case 2: If H1: x̅ > µ, then rejection region lies on upper tail of the T-Distribution (upper-tailed). If the hateful of the sample of interest is greater than the comparison mean. Example: If Component A has a longer time-to-failure than Component B.

In such case, use Upper Tailed based exam.

Hither, P-value = Pr(T > t)

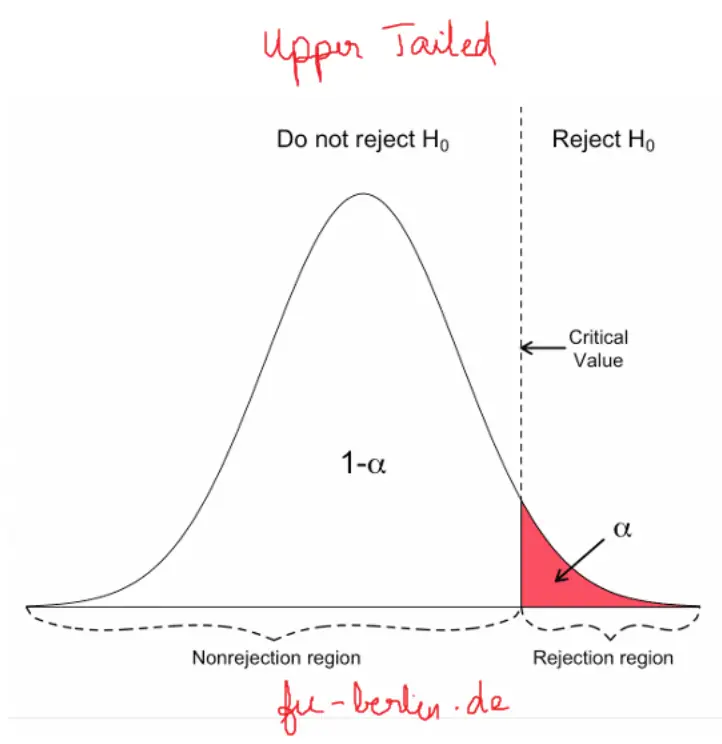
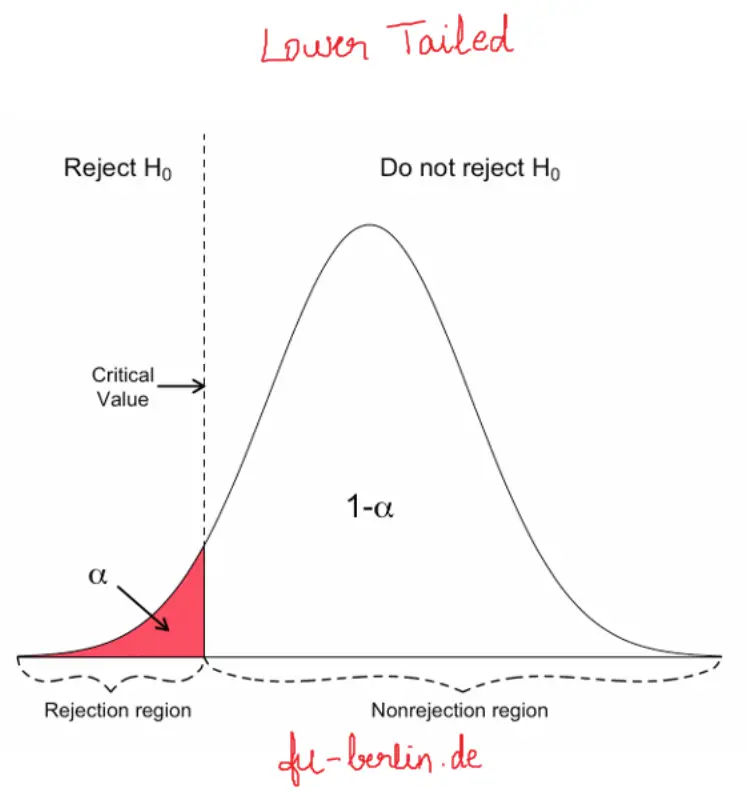
Case 3: If H1: x̅ < µ, then rejection region lies on lower tail of the T-Distribution (lower-tailed). If the mean of the sample of involvement is bottom than the comparison mean.

In such case, utilize lower tailed test.

Here, P-value = Pr(T < t)

Conclusion

Hope you are now familiar and clear about with the One Sample T Test. If some thing is still non clear, write in comment. Next, topic is Two sample T exam. Stay tuned.

allenbenety.blogspot.com

Source: https://www.machinelearningplus.com/statistics/one-sample-t-test/

Share this post